Heuristics
✨ If you ask a chess pro why a chess move is good, they'll probably give you a bunch of reasons, many of them intuitive, about why they made that decision.
It is important to develop your pieces in the opening while trying to control the center of the board at the same time. Castling is an excellent move as long as the king gets safe. Then, in the middlegame space becomes an advantage. And if a complex position can be simplified when you have an advantage, then so much the better. The pawn structure could determine the endgame.
The list of reasons goes on and on.
The mathematician Claude Shannon came to the conclusion that there are more chess moves than atoms in the universe. The game is complex and you need to learn how to make decisions to play chess like a pro. Since no human can calculate more than, let's say 30 moves ahead, it's all about thinking in terms of heuristics.
Heuristics are quick, mental shortcuts that we humans use to make decisions and solve problems in our daily lives. While far from being perfect, heuristics are approximations that help manage cognitive load.
Listed below are the chess heuristics implemented in PHP Chess.
| Heuristic | Description | Evaluation |
|---|---|---|
| Absolute fork | A tactic in which a piece attacks multiple pieces at the same time. It is a double attack. A fork involving the enemy king is an absolute fork. | Chess\Eval\AbsoluteForkEval |
| Absolute pin | A tactic that occurs when a piece is shielding the king, so it cannot move out of the line of attack because the king would be put in check. | Chess\Eval\AbsolutePinEval |
| Absolute skewer | A tactic in which the enemy king is involved. The king is in check, and it has to move out of danger exposing a more valuable piece to capture. Only line pieces (bishops, rooks and queens) can skewer. | Chess\Eval\AbsoluteSkewerEval |
| Advanced pawn | A pawn that is on the fifth rank or higher. | Chess\Eval\AdvancedPawnEval |
| Attack | If a piece is under threat of being attacked, it means it could be taken after a sequence of captures resulting in a material gain. This indicates a forcing move in that a player is to reply in a certain way. On the next turn, it should be defended by a piece or moved to a safe square. The player with the greater number of material points under attack has an advantage. | Chess\Eval\AttackEval |
| Backward pawn | The last pawn protecting other pawns in its chain. It is considered a weakness because it cannot advance safely. | Chess\Eval\BackwardPawnEval |
| Bad bishop | A bishop that is on the same color as most of own pawns. | Chess\Eval\BadBishopEval |
| Bishop outpost | A bishop on an outpost square is considered a positional advantage because it cannot be attacked by enemy pawns, and as a result, it is often exchanged for another piece. | Chess\Eval\BishopOutpostEval |
| Bishop pair | The player with both bishops may definitely have an advantage, especially in the endgame. Furthermore, two bishops can deliver checkmate. | Chess\Eval\BishopPairEval |
| Center | It is advantageous to control the central squares as well as to place a piece in the center. | Chess\Eval\CenterEval |
| Checkability | Having a king that can be checked is usually considered a disadvantage, and vice versa, it is considered advantageous to have a king that cannot be checked. A checkable king is vulnerable to forcing moves. | Chess\Eval\CheckabilityEval |
| Connectivity | The connectivity of the pieces measures how loosely the pieces are. | Chess\Eval\ConnectivityEval |
| Defense | This heuristic evaluates the defensive strength of each side by analyzing how the removal of attacking pieces would affect the opponent's protection. A higher score indicates a stronger defensive position. | Chess\Eval\DefenseEval |
| Diagonal opposition | The same as direct opposition, but the two kings are apart from each other diagonally. | Chess\Eval\DiagonalOppositionEval |
| Direct opposition | A position in which the kings are facing each other being two squares apart on the same rank or file. In this situation, the player not having to move is said to have the opposition. | Chess\Eval\DirectOppositionEval |
| Discovered check | A discovered check occurs when the opponent's king can be checked by moving a piece out of the way of another. | Chess\Eval\DiscoveredCheckEval |
| Doubled pawn | A pawn is doubled if there are two pawns of the same color on the same file. | Chess\Eval\DoubledPawnEval |
| Far-advanced pawn | A pawn that is threatening to promote. | Chess\Eval\FarAdvancedPawnEval |
| Flight square | The safe squares to which the king can move if it is threatened. | Chess\Eval\FlightSquareEval |
| Isolated pawn | A pawn without friendly pawns on the adjacent files. Since it cannot be defended by other pawns it is considered a weakness. | Chess\Eval\IsolatedPawnEval |
| King safety | An unsafe king leads to uncertainty. The probability of unexpected, forced moves will increase as the opponent's pieces get closer to it. | Chess\Eval\KingSafetyEval |
| Knight outpost | A knight on an outpost square is considered a positional advantage because it cannot be attacked by enemy pawns, and as a result, it is often exchanged for a bishop. | Chess\Eval\KnightOutpostEval |
| Material | The player with the most material points has an advantage. The relative values of the pieces are assigned this way: 1 point to a pawn, 3.2 points to a knight, 3.33 points to a bishop, 5.1 points to a rook and 8.8 points to a queen. | Chess\Eval\MaterialEval |
| Overloading | A piece that is overloaded with defensive tasks is vulnerable because it can be deflected, meaning it could be forced to leave the square it occupies, typically resulting in an advantage for the opponent. | Chess\Eval\OverloadingEval |
| Passed pawn | A pawn with no opposing pawns on either the same file or adjacent files to prevent it from being promoted. | Chess\Eval\PassedPawnEval |
| Pressure | This is a measure of the number of squares targeted by each player that require special attention. It often indicates the step prior to an attack. The player with the greater number of them has an advantage. | Chess\Eval\PressureEval |
| Protection | If a piece is unprotected, it means that there are no other pieces defending it, and therefore it can be taken for free resulting in a material gain. This indicates a forcing move in that a player is to reply in a certain way. On the next turn, it should be defended by a piece or moved to a safe square. The player with the greater number of material points under protection has an advantage. | Chess\Eval\ProtectionEval |
| Relative fork | A tactic in which a piece attacks multiple pieces at the same time. It is a double attack. A fork not involving the enemy king is a relative fork. | Chess\Eval\RelativeForkEval |
| Relative pin | A tactic that occurs when a piece is shielding a more valuable piece, so if it moves out of the line of attack the more valuable piece can be captured resulting in a material gain. | Chess\Eval\RelativePinEval |
| Space | This is a measure of the number of squares controlled by each player. | Chess\Eval\SpaceEval |
| Square outpost | A square protected by a pawn that cannot be attacked by an opponent's pawn. | Chess\Eval\SqOutpostEval |
Evaluate a Chess Position
Chess\EvalArray allows to transform a FEN position to a normalized array of values between -1 and +1. -1 is the best possible evaluation for Black and +1 the best possible evaluation for White. Both forces being set to 0 means they're balanced.
use Chess\EvalArray;
use Chess\FenToBoardFactory;
use Chess\Function\CompleteFunction;
$f = new CompleteFunction();
$fen = 'rnbqkb1r/p1pp1ppp/1p2pn2/8/2PP4/2N2N2/PP2PPPP/R1BQKB1R b KQkq -';
$board = FenToBoardFactory::create($fen);
$result = [
'names' => $f->names(),
'normd' => EvalArray::normalization($f, $board),
];
print_r($result);
Array
(
[names] => Array
(
[0] => Material
[1] => Center
[2] => Connectivity
[3] => Space
[4] => Pressure
[5] => King safety
[6] => Protection
[7] => Discovered check
[8] => Doubled pawn
[9] => Passed pawn
[10] => Advanced pawn
[11] => Far-advanced pawn
[12] => Isolated pawn
[13] => Backward pawn
[14] => Defense
[15] => Absolute skewer
[16] => Absolute pin
[17] => Relative pin
[18] => Absolute fork
[19] => Relative fork
[20] => Outpost square
[21] => Knight outpost
[22] => Bishop outpost
[23] => Bishop pair
[24] => Bad bishop
[25] => Diagonal opposition
[26] => Direct opposition
[27] => Overloading
[28] => Back-rank threat
[29] => Flight square
[30] => Attack
[31] => Checkability
)
[normd] => Array
(
[0] => 0
[1] => 1
[2] => -1
[3] => 0.2419
[4] => 0
[5] => 0
[6] => 0
[7] => 0
[8] => 0
[9] => 0
[10] => 0
[11] => 0
[12] => 0
[13] => 0
[14] => 0
[15] => 0
[16] => 0
[17] => 0
[18] => 0
[19] => 0
[20] => 0
[21] => 0
[22] => 0
[23] => 0
[24] => 0
[25] => 0
[26] => 0
[27] => 0
[28] => 0
[29] => 0
[30] => 0
[31] => 0
)
)
This data structure is used to estimate who may be better without considering checkmate. Please note that a heuristic evaluation is not the same thing as a chess calculation. Heuristic evaluations are often correct but may fail because they are based on probabilities.
Steinitz Evaluation
As chess champion William Steinitz pointed out, a strong position can be created by accumulating small advantages. The relative value of the position without considering checkmate is obtained by counting the advantages in the evaluation array.
$steinitz = EvalArray::steinitz($f, $board);
echo $steinitz;
1
In this example, White is better than Black because the value obtained is a positive number. One evaluation feature is favoring White.
Chess evaluation functions often consist in multiplying the terms by a weight and adding the results to construct a linear combination.
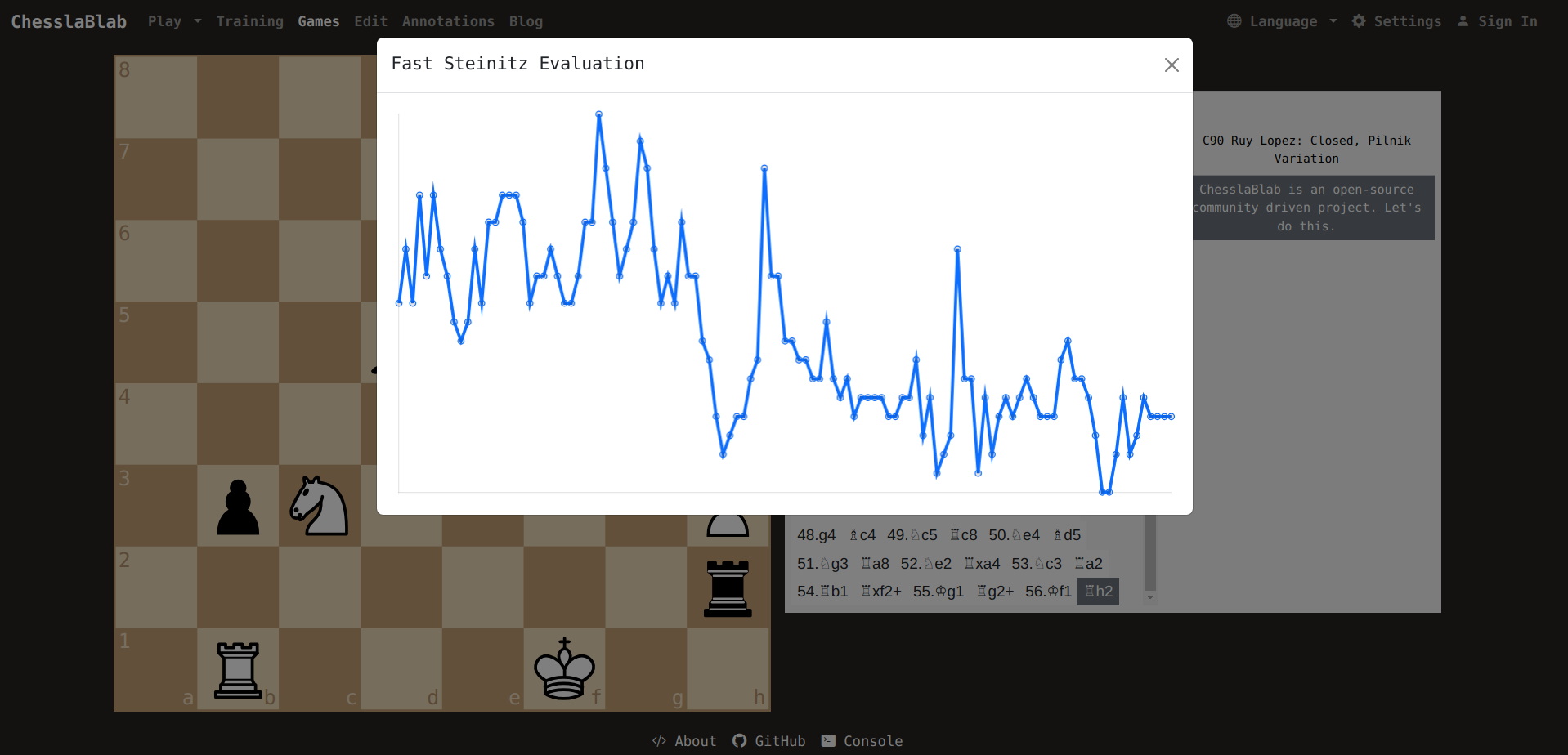
However, the Steinitz evaluation alone, which is to say just counting the advantages, has proven to be quite accurate as a relative estimate for chess positions in a way that is easy for human players to understand and to learn. Also it can be complemented with other statistical measures such as the mean, median, mode, and standard deviation of the evaluation array without counting the zeros.
Mean
The mean represents the center of the evaluation array being intermediate to the extreme values.
$mean = EvalArray::mean($f, $board);
echo $mean;
0.0806
Median
The median is the value in the middle of the evaluation array.
$median = EvalArray::median($f, $board);
echo $median;
0.2419
Mode
The mode is the value that appears most frequently in the evaluation array.
$mode = EvalArray::mode($f, $board);
echo $mode;
In this example, no mode exists since there are no repeating numbers in the evaluation array.
Standard Deviation
The standard deviation is a measure of how spread out the evaluation array is.
$sd = EvalArray::sd($f, $board);
echo $sd;
0.8244
Plot the Oscillations of a Game
Given a PGN movetext in SAN format, Chess\SanPlotter returns the oscillations of an evaluation feature in the time domain.
use Chess\SanPlotter;
use Chess\Function\CompleteFunction;
use Chess\Variant\Classical\Board;
$f = new CompleteFunction();
$board = new Board();
$movetext = '1.e4 d5 2.exd5 Qxd5';
$name = 'Space';
$time = SanPlotter::time($f, $board, $movetext, $name);
print_r($time);
Array
(
[0] => 0
[1] => 1
[2] => 0.25
[3] => 0.5
[4] => -1
)
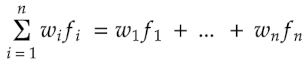
The data is plotted in a way that is easy for chess players to understand and learn.
Extract Chess Data
Chess\SanExtractor extracts oscillations data for further analysis like the following example.
use Chess\SanExtractor;
use Chess\Function\CompleteFunction;
use Chess\Variant\Classical\Board;
$f = new CompleteFunction();
$board = new Board();
$movetext = '1.e4 d5 2.exd5 Qxd5';
Evaluation Array
This is how component number four, which is to say the normalization of the fourth evaluation array, is obtained from the example above.
$eval = SanExtractor::eval($f, $board, $movetext);
print_r($eval[4]);
Array
(
[0] => 0
[1] => -1
[2] => 1
[3] => -0.2423
[4] => -0.0661
[5] => -0.022
[6] => 0
[7] => 0
[8] => 0
[9] => 0
[10] => 0
[11] => 0
[12] => 0
[13] => 0
[14] => -0.1123
[15] => 0
[16] => 0
[17] => 0
[18] => 0
[19] => 0
[20] => 0
[21] => 0
[22] => 0
[23] => 0
[24] => 0
[25] => 0
[26] => 0
[27] => 0
[28] => 0
[29] => -0.022
[30] => 0
[31] => 0
)
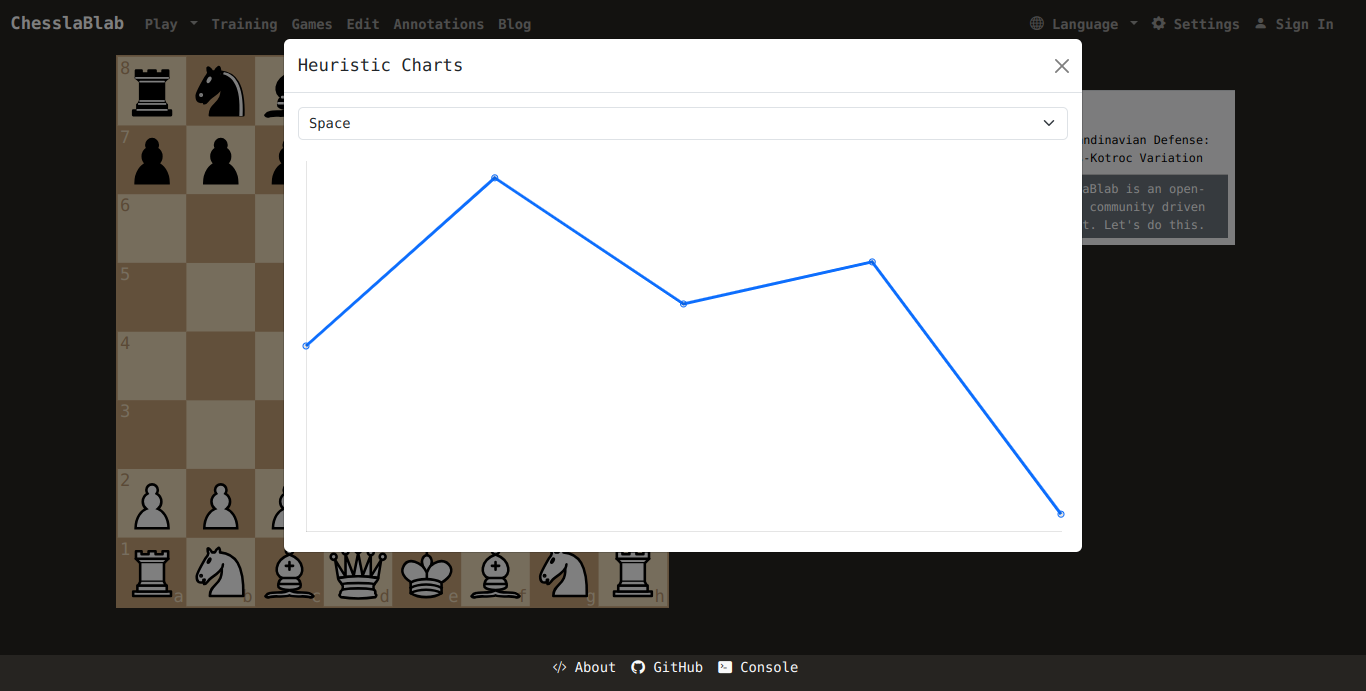
The evaluation array can be plotted in a way that is easy for chess players to understand and learn.
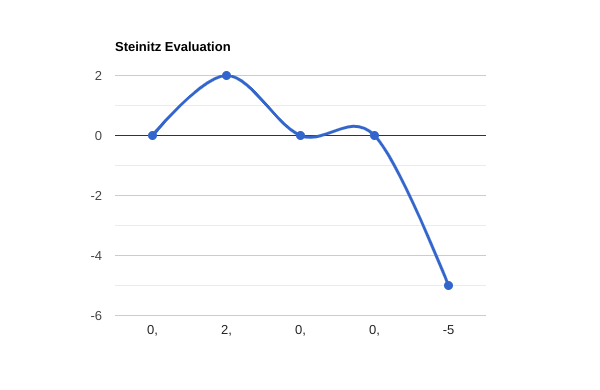
Steinitz Evaluation
$steinitz = SanExtractor::steinitz($f, $board, $movetext);
print_r($steinitz);
Array
(
[0] => 0
[1] => 2
[2] => 0
[3] => 0
[4] => -5
)
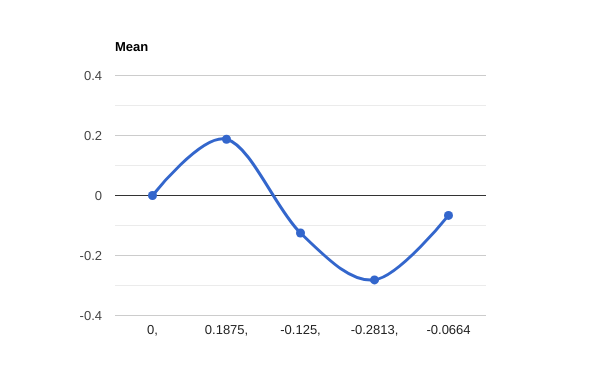
Mean
$mean = SanExtractor::mean($f, $board, $movetext);
print_r($mean);
Array
(
[0] => 0
[1] => 0.1875
[2] => -0.1667
[3] => -0.3125
[4] => -0.0664
)
Standard Deviation
$sd = SanExtractor::sd($f, $board, $movetext);
print_r($sd);
Array
(
[0] => 0
[1] => 0.7601
[2] => -0.8498
[3] => -0.7294
[4] => -0.5406
)
🎉 So chess positions and games can be plotted on charts and processed with machine learning techniques. Become a better player by extracting knowledge from games with the help of Data Mining tools.